This demonstration is designed to illustrate the link between the formulae for volume of a cylinder, a cone and a sphere.
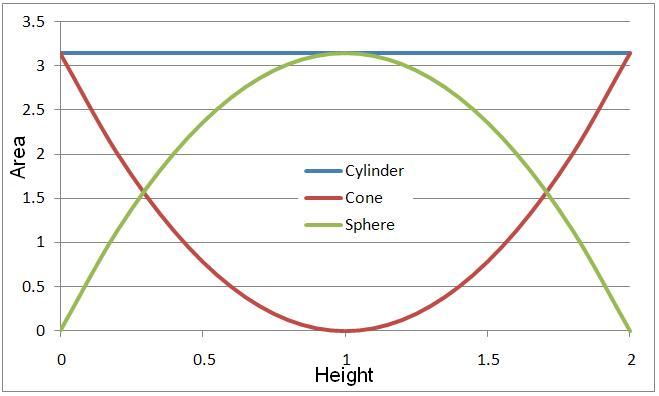
Taking a cross-section of each of the shapes below at various heights we can see that the area of the circle cut from the cylinder is equal to the area of the circles cut from the cones and sphere put together. The following graph shows how the area of each varies with the height of the cut:
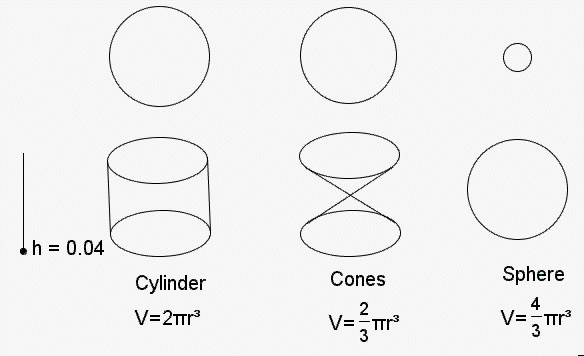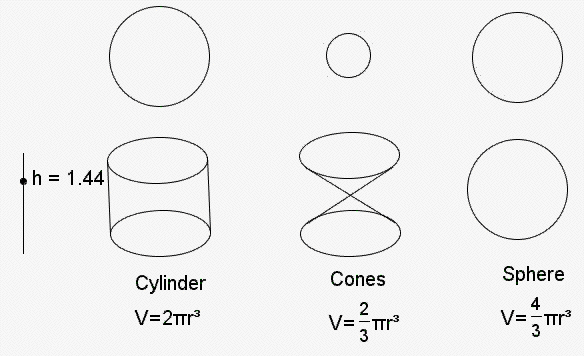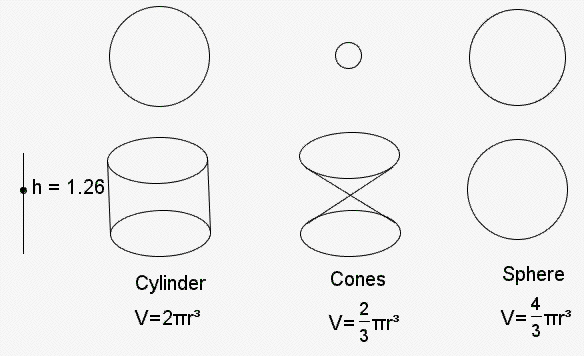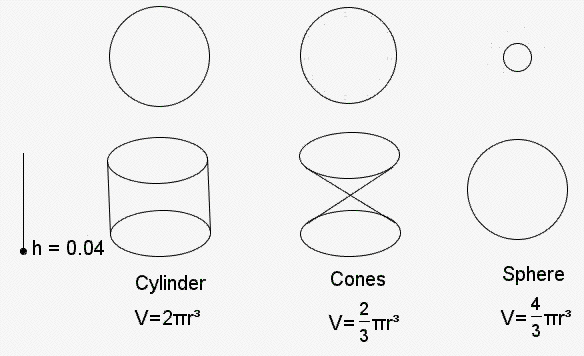
Taking a cross-section of each of the shapes below at various heights we can see that the area of the circle cut from the cylinder is equal to the area of the circles cut from the cones and sphere put together. The following graph shows how the area of each varies with the height of the cut:
As the height, h, varies, the area of the cross-sectional circle for each shape varies accordingly:
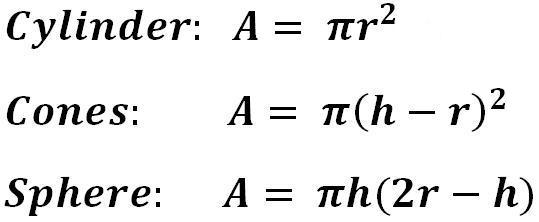
Taking a cross-section of each of the shapes below at various heights we can see that the area of the circle cut from the cylinder is equal to the area of the circles cut from the cones and sphere put together. The following graph shows how the area of each varies with the height of the cut:

Taking a cross-section of each of the shapes below at various heights we can see that the area of the circle cut from the cylinder is equal to the area of the circles cut from the cones and sphere put together. The following graph shows how the area of each varies with the height of the cut:

As the height, h, varies, the area of the cross-sectional circle for each shape varies accordingly:
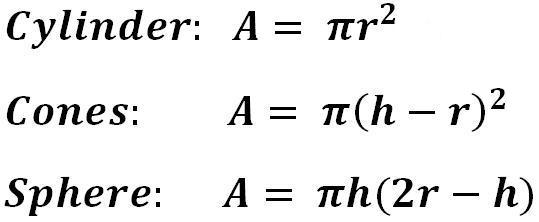
From
these it can be shown algebraically that the area of the cones and the
sphere do add up to the area of the cylinder, and if this is the case
then the volumes must also add up to the volume of the cylinder.
________________________________________________________________________
